Enjoy With Matematic

Standar Kompetensi :

Memahami bentuk aljabar dan menggunakannya dalam pemecahan masalah.

Kompetensi Dasar;

Melakukan Operasi aljabar.

Menguraikan Bentuk Aljabar ke dalam Faktor-faktornya.

Tujuan pembelajaranmu pada bab ini adalah:

Dapat menyelesaikan operasi tambah, kurang, kali, bagi, dan pangkat pada bentuk aljabar;

Dapat menentukan faktor suku aljabar;

Dapat menguraikan bentuk aljabar ke dalam faktor-faktornya.

Materi :

Sebelum mempelajari faktorisasi suku aljabar, marilah kita ingat kembali istilah-istilah yang terdapat pada bentuk aljabar.

Variabel

Variabel adalah lambang pengganti suatu bilangan yang belum diketahui nilainya dengan jelas. Variabel disebut juga peubah. Variabel biasanya dilambangkan dengan huruf kecil a, b, c, ... z.

Konstanta

Suku dari suatu bentuk aljabar yang berupa bilangan dan tidak memuat variabel disebut konstanta.

Koefisien

Koefisien pada bentuk aljabar adalah faktor konstanta dari suatu suku pada bentuk aljabar.

Suku

Suku adalah variabel beserta koefisiennya atau konstanta pada bentuk aljabar yang dipisahkan oleh operasi jumlah atau selisih.

Suku satu adalah bentuk aljabar yang tidak dihubungkan oleh operasi jumlah atau selisih. Contoh:

Suku dua adalah bentuk aljabar yang dihubungkan oleh satu operasi jumlah atau selisih. Contoh:

Suku tiga adalah bentuk aljabar yang dihubungkan oleh dua operasi jumlah atau selisih. Contoh:

Bentuk aljabar yang mempunyai lebih dari dua suku disebut suku banyak atau polinom. Nanti, di tingkat yang lebih lanjut kalian akan mempelajari mengenai suku banyak atau polinom.

LATIHAN SOAL KONSTANTA.pptx
OPERASI HITUNG PADA BENTUK ALJABAR

Penjumlahan dan Pengurangan Bentuk Aljabar

Pada bagian ini, kamu akan mempelajari cara menjumlahkan dan mengurangkan suku-suku sejenis pada bentuk aljabar. Pada dasarnya, sifat-sifat penjumlahan dan pengurangan yang berlaku pada bilangan riil, berlaku juga untuk penjumlahan dan pengurangan pada bentuk-bentuk aljabar, sebagai berikut.

Sifat Komutatif

a + b = b + a, dengan a dan b bilangan riil

Sifat Asosiatif

(a + b) + c = a + (b +c), dengan a, b, dan c bilangan riil

Sifat Distributif

a (b + c) = ab + ac, dengan a, b, dan c bilangan riil

Perkalian Bentuk Aljabar

Perkalian Suatu Bilangan dengan Bentuk Aljabar

Coba kalian ingat kembali sifat distributif pada bilangan bulat. Jika a , b , dan c bilangan bulat maka berlaku a ( b + c ) = ab + ac . Sifat distributif ini dapat dimanfaatkan untuk menyelesaikan operasi perkalian pada bentuk aljabar.

Perkalian suku dua ( ax + b ) dengan skalar/bilangan k dinyatakan sebagai berikut.

k ( ax + b ) = kax + kb

Perkalian antara Bentuk aljabar dan Bentuk Aljabar

Telah dipelajari bahwa perkalian antara bilangan scalar k dengan suku dua ( ax + b ) adalah k ( ax + b ) = kax + kb. Dengan memanfaatkan sifat distributif pula, perkalian antara bentuk aljabar suku dua ( ax + b ) dengan suku dua ( ax + d ) diperoleh sebagai berikut.

(ax+b)(cx+d)=ax(cx+d)+b(cx+d)

=ax(cx)+ax(d)+b(cx)+bd

=

Sifat distributif dapat pula digunakan pad perkalian suku dua dan suku tiga.

Pembagian Bentuk Aljabar

Pada operasi pembagian bentuk aljabar kalian harus menentukan terlebih dahulu faktor sekutu kedua bentuk aljabar tersebut, kemudian baru dilakukan pembagian. Pembagian bentuk aljabar akan lebih mudah jika dinyatakan dalam bentuk pecahan.

Perpangkatan Bentuk Aljabar

Operasi perpangkatan diartikan sebagai operasi perkalian berulang dengan unsure yang sama. Untuk sebarang bilangan bulat a , berlaku :

.

Sekarang kalian akan mempelajari operasi perpangkatan pada bentuk aljabar. Untuk memudahkan penguraian perpangkatan bentuk-bentuk aljabar tersebut, kamu bisa menggunakan pola segitiga Pascal . Sekarang, perhatikan pola segitiga Pascal berikut.

Hubungan antara segitiga Pascal dengan perpangkatan suku dua bentuk aljabar adalah sebagai berikut.

Perpangkatan bentuk aljabar 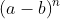dengan n bilangan asli juga mengikuti pola segitiga Pascal. Akan tetapi, tanda setiap koefisiennya selalu berganti dari (+) ke (–), begitu seterusnya.

LATIHAN SOAL ALJABAR.pptx
PEMFAKTORAN BENTUK ALJABAR

Pemfaktoran atau faktorisasi bentuk aljabar adalah menyatakan bentuk penjumlahan menjadi suatu bentuk perkalian dari bentuk aljabar tersebut.

Pemfaktoran dengan Sifat Distributif

Pada dasarnya, memfaktorkan suatu bilangan berarti menyatakan suatu bilangan dalam bentuk perkalian faktor-faktornya. Pada bagian ini, akan dipelajari cara-cara memfaktorkan suatu bentuk aljabar dengan menggunakan sifat distributif. Dengan sifat ini, bentuk aljabar ax + ay dapat difaktorkan menjadi a(x + y), di mana a adalah faktor persekutuan dari ax dan ay.

Selisih Dua Kuadrat

Perhatikan bentuk perkalian (a + b)(a – b). Bentuk ini dapat ditulis

Jadi, bentuk dapat dinyatakan dalam bentuk perkalian (a + b) (a – b).

.

Bentuk disebut selisih dua kuadrat

Pemfaktoran Bentuk Kuadrat

Pemfaktoran bentuk dengan a = 1

Perhatikan perkalian suku dua berikut.

Jadi, bentuk dapat difaktorkan menjadi (x + p)(x + q)

Misalkan, 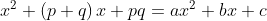sehingga a = 1, b = p + q, dan c = pq. Dari pemisalan tersebut, dapat dilihat bahwa p dan q merupakan factor dari c. Jika p dan q dijumlahkan, hasilnya adalah b. Dengan demikian untuk memfaktorkan bentuk 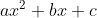dengan a = 1, tentukan dua bilangan yang merupakan faktor dari c dan apabila kedua bilangan tersebut dijumlahkan, hasilnya sama dengan b.

Pemfaktoran Bentuk dengan a≠1

Sebelumnya, kamu telah memfaktorkan bentuk 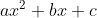dengan a = 1. Sekarang kamu akan mempelajari cara memfaktorkan bentuk 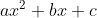dengan a≠1

Perhatikan perkalian suku dua berikut.

Dengan kata lain, bentuk 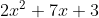difaktorkan menjadi ( x + 3 )( 2x + 1). Adapun cara memfaktorkan 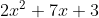adalah dengan membalikkan tahapan perkalian suku dua di atas.

=

= x(2x+1)+3(2x+1)

= ( x + 3 )( 2x + 1)

Dari uraian tersebut dapat kamu ketahui cara memfaktorkan bentuk dengan a≠1 sebagai berikut.

1) Uraikan bx menjadi penjumlahan dua suku yang apabila kedua suku tersebut dikalikan hasilnya sama dengan ( c)

2) Faktorkan bentuk yang diperoleh menggunakan sifat distributif.

LATIHAN SOAL PEMFAKTORAN.pptx
PECAHAN DALAM BENTUK ALJABAR

Penjumlahan dan Pengurangan Pecahan Bentuk Aljabar

Cara menjumlahkan dan mengurangkan pecahan bentuk aljabar adalah sama dengan menjumlahkan dan mengurangkan pada pecahan biasa, yaitu dengan menyamakan penyebutnya terlebih dahulu.

Perkalian dan Pembagian Pecahan Bentuk Aljabar

Perkalian

Cara mengalikan pecahan bentuk aljabar sama dengan mengalikan pecahan biasa, yaitu

dengan b≠0 dan d≠0

Pembagian

Aturan pembagian pada pecahan bentuk aljabar sama dengan aturan pembagian pada pecahan biasa, yaitu :

dengan b≠0 dan d≠0

Perpangkatan Pecahan Bentuk Aljabar

Pada bagian sebelumnya, kamu telah mengetahui bahwa untuk a bilangan riil dan n bilangan asli, berlaku:

.

Definisi blangan berpangkat tersebut berlaku juga pada pecahan bentuk aljabar.

Penyederhanaan Pecahan Bentuk Aljabar

Pecahan dikatakan sederhana jika pembilang dan penyebut pecahan tersebut tidak lagi memiliki faktor persekutuan, kecuali 1. Dengan kata lain, jika pembilang dan penyebut suatu pecahan memiliki faktor yang sama kecuali 1 maka pecahan tersebut dapat disederhanakan. Hal ini juga berlaku pada pecahan bentuk aljabar. Menyederhanakan pecahan aljabar dapat dilakukan dengan memfaktorkan pembilang dan penyebutnya terlebih dahulu, kemudian dibagi dengan faktor sekutu dari pembilang dan penyebut tersebut.

Menyederhanakan Pecahan Bersusun (Kompleks)

Pecahan bersusun (kompleks) adalah suatu pecahan yang pembilang atau penyebutnya atau kedua-duanya masih memuat pecahan. Untuk menyederhanakan pecahan bersusun, dilakukan dengan cara mengalikan pembilang dan penyebutnya dengan KPK dari penyebut pecahan pada pembilang dan penyebut pecahan pada penyebut pecahan bersusun.